Git-Ring: Easy & Flexible SSH Ring Signatures.

This is the companion post to a tool, git-ring, that I recently released on Github.

Github/Gitlab makes the public keys of its users publicly available (at github.com/USERNAME.keys and gitlab.com/USERNAME.keys), this means that these services bind the users identity to public keys via this endpoint. Git-ring “exploits” this to enable the creation of (cryptographic) proofs showing membership among a set of users (or organizations) without revealing the identity of the person generating the proof. The public keys of everyone (including the signer) is automatically downloaded from Github, while the tool finds the correct private key on the signers local computer. All this combined makes using the tool pretty easy, as shown below, where we sign a message and then verify the resulting signature.

More examples can be found in the Github repository. The tool also supports manually supplying SSH public keys.

Git-ring is useful for things like whistleblowing: by signing a leak using git-ring an anonymous person proves that it originates from someone within the organization and hence the claims are likely authentic – without revealing their identity to anyone. The goal of this post is to give a quick behind-the-scenes look at how the (relatively simple) underlying cryptography works.

Ring Signatures

Git-ring uses ring signatures to implement the attestations described above. A ring signature scheme is like a regular digital signature scheme, except signing now additionally takes a set of public keys among which the real signer is hiding their identity i.e. the real signer is among the set of public keys, but the resulting signature does not reveal their identity (their public key). In other words the signing algorithm takes:

1. A set of public keys \( \pk_1, \ldots, \pk_n \) of potential signers (called “the anonymity set” or “the ring”).
2. The secret key \( \sk \) of the actual signer.
3. The message \( \msg \) to sign.

And returns a digital signature, in other symbols:

\[ \sig \gets \sign(\{ \pk_1, \ldots, \pk_n \}, \sk, \msg) \]

Unlike a regular digital signature scheme, verification now takes a set of public keys (instead of a single key):

\[ \bin \gets \verify(\{ \pk_1, \ldots, \pk_n \}, \sig, \msg) \]

For security, a ring signature scheme must satisfy anonymity and unforgability, which informally stated requires:

(Strong) Anonymity: \(\sig\) hides which of the signers \( \pk_1, \ldots, \pk_n \) created the signature (i.e. which \( \pk_i \) the \( \sk \) belongs to), even if the adversary has access to all the secret keys. This means privacy even in e.g. the scenario where an authority demands to get everyone’s secret keys (including the real signer’s) in an attempt to uncover the real signer.

(Strong) Unforgability: If the signer does not know the secret key for one of the public keys \( \pk_1, \ldots, \pk_n \), he cannot produce a new valid signature \( \sig \) on any message \( \msg \), i.e. produce \(\sig\) such that \( \verify(\{ \pk_1, \ldots, \pk_n \}, \sig, \msg) = 1 \). This remains the case, even if the attacker is provided with previously valid signatures \( \sig_1’, \ldots, \sig_k’ \) where \( \forall i. \sig \neq \sig_i’ \).

While the original paper conceiving ring signatures by Rivest, Shamir and Tauman describes a construction based on RSA and only works for RSA keys. Git-ring instead use a generic technique by Cramer, Damgård and Schoenmakers based on Sigma protocols together with the Fiat-Shamir heuristic. This enables git-ring to include any mix of SSH keys (of different types) in the same ring, making it much more flexible.

To understand the construction we start by describing (loosely) what sigma protocols are.

Intro to \(\Sigma\)-Protocols

\(\Sigma\)-protocols are especially simple/elegant classes of (public-coin interactive) zero-knowledge proofs-of-knowledge.

They have three rounds of communication:

1. Prover sends a message (often called “the commitment”). Denoted “a”.
2. The verifier sends a uniformly random challenge. Denoted “c”.
3. The prover sends a response. Denoted “z”.

The verifier ends by checking the “validity” of the transcript \( (a, c, z) \) against the statement (public key) and rejecting/accepting. The communication pattern is illustrated below (P for Prover and V for Verifier):

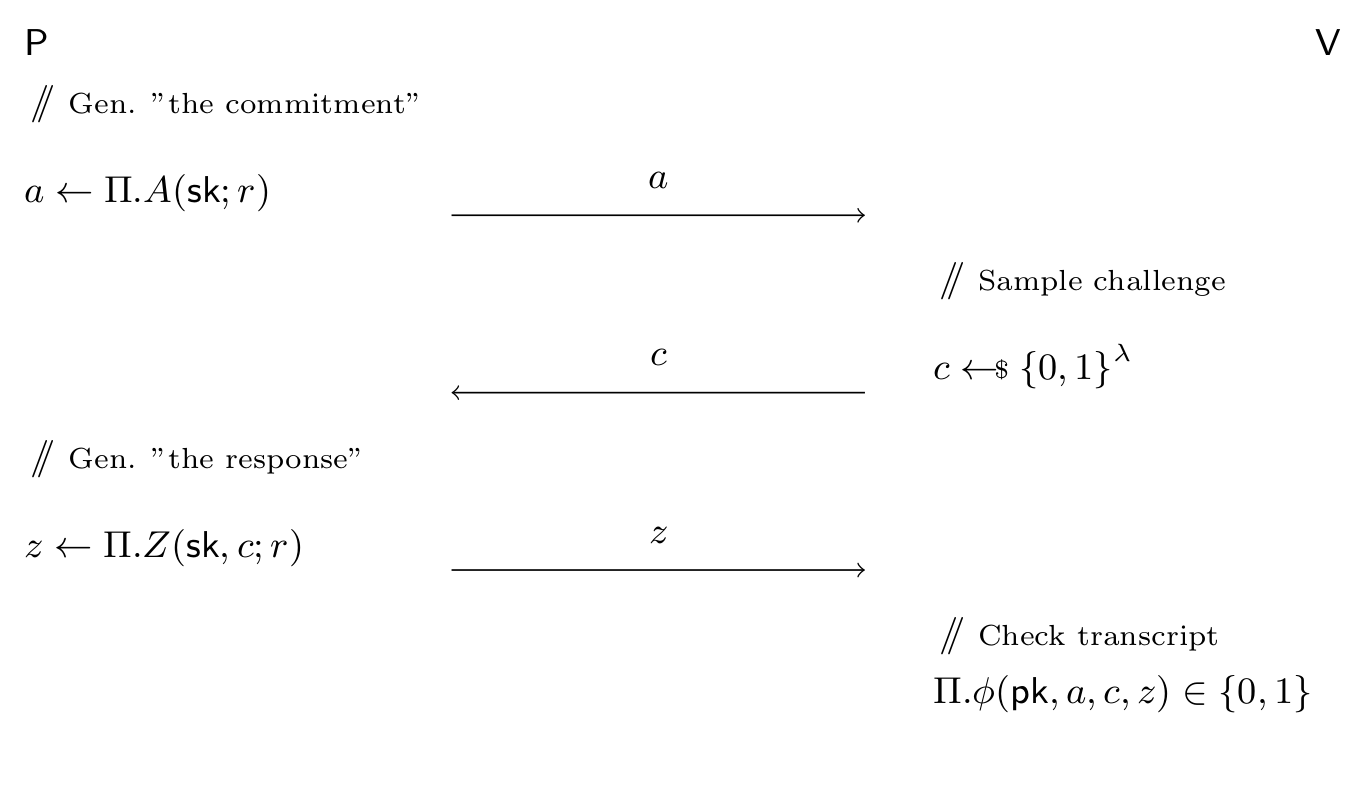
We require knowledge soundness, which informally states that a prover which does not know a witness (secret key) almost always fails to make the verifier accept. However for the purpose of this post, the most interesting feature of \(\Sigma\)-protocols is that they are “special-honest verifier zero-knowledge”, meaning that there exists a simulator: an efficient algorithm which given the challenge \(c\) produces complete transcripts \((a, c, z)\) which have the same distribution as the honest interaction. The only “special” power that the simulator has over the prover is the ability to sample \( a \) after seeing \( c \), whereas the prover has to send \( a \) to the verifier before receiving \( c \).

\(\Sigma\)-Protocol for ECDSA and EdDSA Keys

Schnorr’s identification protocol is the quintessential example of \(\Sigma\)-protocol. It proves knowledge of the discrete log in a cyclic group, i.e. that the prover knows \(x\) st. \( \pk = [x] \cdot G \) for group elements \( \pk, G \) where we use the additive notation for the group operation. It operates as follows:

1. Prover samples \( r \sample \ZZ_{|\GG|} \), computes \( a = [r] \cdot G \) sends \( a \in \GG \) to the verifier.
2. Verifier sends \( c \sample \ZZ_{|\GG|} \) to the verifier.
3. Prover responds with \( z = c \cdot x + r \in \ZZ_{|\GG|} \)

Finally the verifier checks: \[ [z] \cdot G = [c] \cdot \mathsf{pk} + a \in \GG \] Pictorially it looks as follows:

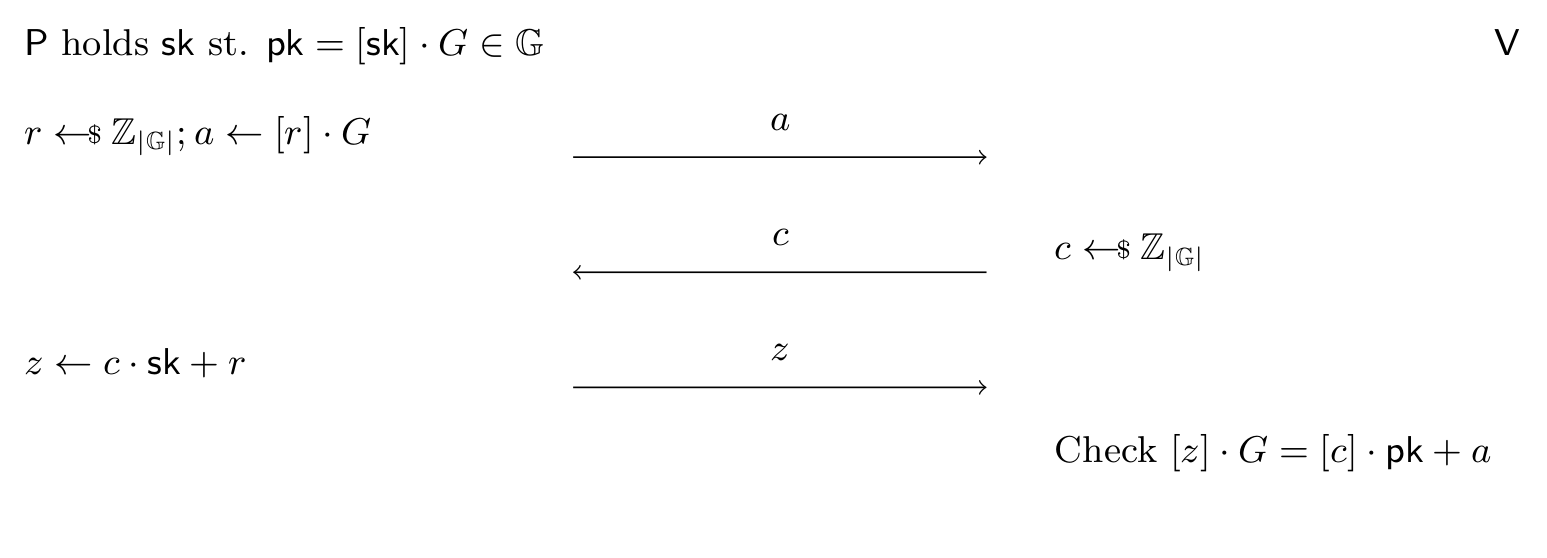
Note the protocol above works for any cyclic group of known order, hence we can instantiate it with both edwards25519 or the NIST curves P-256/P-384/P-521 to show knowledge of an Ed25519 or ECDSA key respectively.

Soundness: To see why the protocol above is sound consider a prover which, after sending \( a \), could answers two different verifier challenges \( c_1, c_2 \) with \( z_1, z_2 \) such that both \( [z_1] \cdot G = [c_1] \cdot \pk + a \) and \( [z_2] \cdot G = [c_2] \cdot \pk + a \), in other words: there exists at least two challenges for which the prover can convince the verifier. Then the secret key can be obtained as follows:

1. Subtract \( [z_2] \cdot G = [c_2] \cdot \pk + a \) from \( [z_1] \cdot G = [c_1] \cdot \pk + a \) which eliminates \( a \):

\[ [z_1 - z_2] \cdot G = [c_1 - c_2] \cdot \pk \]

2. Divide by \( c_1 - c_2 \) (which is non-zero since \(c_1 \neq c_2 \)) on both sides:

\[ \pk = \left[ \frac{ z_1 - z_2 }{ c_1 - c_2 } \right] \cdot G \] Hence \( \sk = (z_1 - z_2) \cdot (c_1 - c_2)^{-1} \)

The intuition for the section above is as follows: if the prover could answer two different challenges \( c_1, c_2 \) after sending \( a \), then they could also efficiently compute the secret key \( \sk \) (as shown above), hence a prover which does not know \( \sk \) can answer at most 1 challenge for each \( a \): therefore any cheating prover fails with probability \( 1 - \frac{1}{|\GG|} \).

Simulation: On the other hand, given \( c \) it is easy to sample \( z, a \) st. \( [z] \cdot G = [c] \cdot \mathsf{pk} + a \in \GG \) without knowing \( \sk \) as follows:

1. Pick \( z \sample \ZZ_{|\GG|} \) at random.
2. Solve \( [z] \cdot G = [c] \cdot \pk + a \) (the verifiers check) by setting \( a = [z] \cdot G - [c] \cdot \pk \in \GG \)

\(\Sigma\)-Protocol for RSA Keys

Since RSA keys are still quite popular among SSH users we also need a way to prove knowledge of an RSA private key in such a way that we create a “cheating” proof if we know the challenge \( c \) a head of time. The idea for this protocol is simple: the hard problem in RSA is to invert a permutation \( \psi: \ZZ_{N}^* \to \ZZ_{N}^* \) (with \( \psi(x) = x^e \mod N \)) which can computed efficiently in the forward direction. Therefore to convince the verifier that the prover holds the secret key (and can therefore invert the permutation), we let the verifier sample a random element \( t \in \ZZ_N \) for the prover to invert, the proof is the inverse \( z \), which the verifier can check by simply computing the permutation in the forward direction. i.e. check:

\[ t \overset?= \psi(z) \]

Since the verifiers challenge \( t \) is chosen uniformly at random the protocol above convinces the verifier that the prover can invert the permutation with good probability, however it does not allow simulation – it’s not zero-knowledge.

Therefore instead of having the verifier send \( t \) we form \( t = c + a \) where the prover first chooses \( a \in \ZZ_N \) and the verifier then samples \( c \in \ZZ_N \). This enables choosing \( t \) arbitrarily by modifying \( a \) if \( c \) is know ahead of time, however if \( a \) must be chosen first then the prover cannot control \( t \) and its distribution is uniform over \( c \).

The protocol is verify simple:

1. Prover samples random \(a \sample \ZZ_N\), sends \( a \) to the verifier.
2. Verifier sends \( c \sample \ZZ_N \) to the prover, define \( t = c + a \in \ZZ_N \)
3. Prover sends \( z = \psi^{-1}(t) \in \ZZ_N \)

Verifier checks \( \psi(z) = t \in \ZZ_N \). Pictorially:

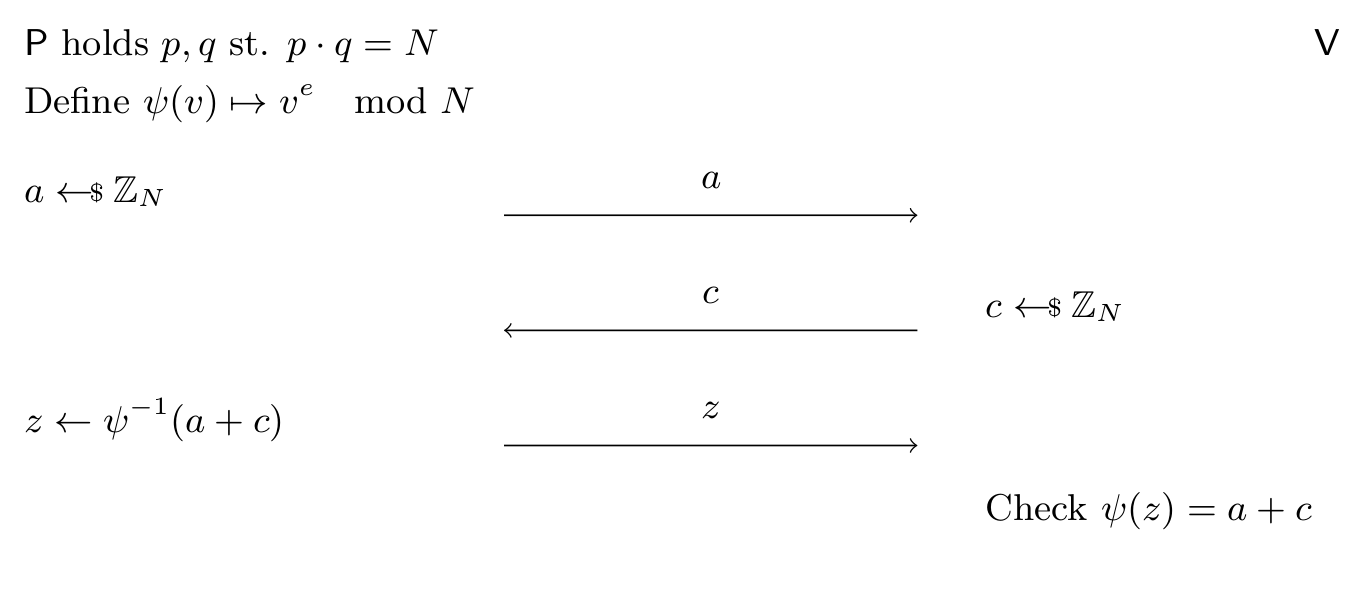
Note \( t \in \ZZ_N \) may not be in \( \ZZ_N^* \); the range of \( \psi \), however in that case you can factor the modulus \( N = p \cdot q \) as \( p = \text{gcd}(t, N) \), therefore this only occurs with negligible probability – so we can ignore this case. Likewise the case of \( t = 0 \) occurs with negligible probability.

Soundness: This protocol is not technically a \(\Sigma\)-protocol: it does not allows extraction of the private key given two different responses to different challenges and the same message. However convincing the verifier does, trivially, reduce to inverting the RSA permutation: after sending \( a \), the verifier can make the prover invert any element \( t \) by picking \( c = t - a \in \ZZ_N \), hence, if the prover succeeds with probability \(\epsilon\) he must be able to invert \( \psi(\cdot) \) on an \(\epsilon\)-fraction of \( \ZZ_N \).

Simulation: given \( c \), we can simulate an accepting transcript without inverting \( \psi \) as follows:

1. Pick \( z \sample \ZZ_N \).
2. Compute \( t \gets \psi(z) \in \ZZ_N \)
3. Compute \( a \gets t - c \in \ZZ_N \)

This way \( a + c = t - c + c = t = \psi(z) \) and the verifier accepts.

At this point we have interactive protocols enabling us to show that we know the private key corresponding to a particular SSH public key, but how do we show that we know a private key for one of many SSH public keys? Also how do we convert these interactive protocol into a signature?

Let’s deal with these two issues one at a time.

CDS Protocol Compiler: Proofs of Partial Knowledge.

Suppose you have a set of \( n \) public keys \( \pk_1, \ldots, \pk_n \) and you want to prove that you know a secret key \( \sk_\alpha \) corresponding to one of the public keys \( \pk_\alpha \). Furthermore, you have (possibly distinct, possibly not) \( \Sigma \)-protocols \( \Pi_1, \ldots, \Pi_n \) (for example the two described above) enabling you to prove knowledge of \( \sk_i \) for \( \pk_i \) using the protocol \( \Pi_i \). e.g. prove that you possess the \( \texttt{Ed25519} \) secret key of a \( \texttt{Ed25519} \) public key \( \pk_i \).

Obviously, the prover could just tell the verifier which index \( \alpha \) he has the secret key for, then the prover and verifier run \( \Pi_\alpha \) to prover/verify this fact. The obvious problem with the obvious protocol is that it leaks \( \alpha \): the verifier learns which public key the prover has a secret key for; this is bad, as it would allow anyone with the ring signature to trivially find out who signed the message :(

This problem is solved simply and elegantly by Cramer, Damgård and Schoenmakers. The idea is as follows:

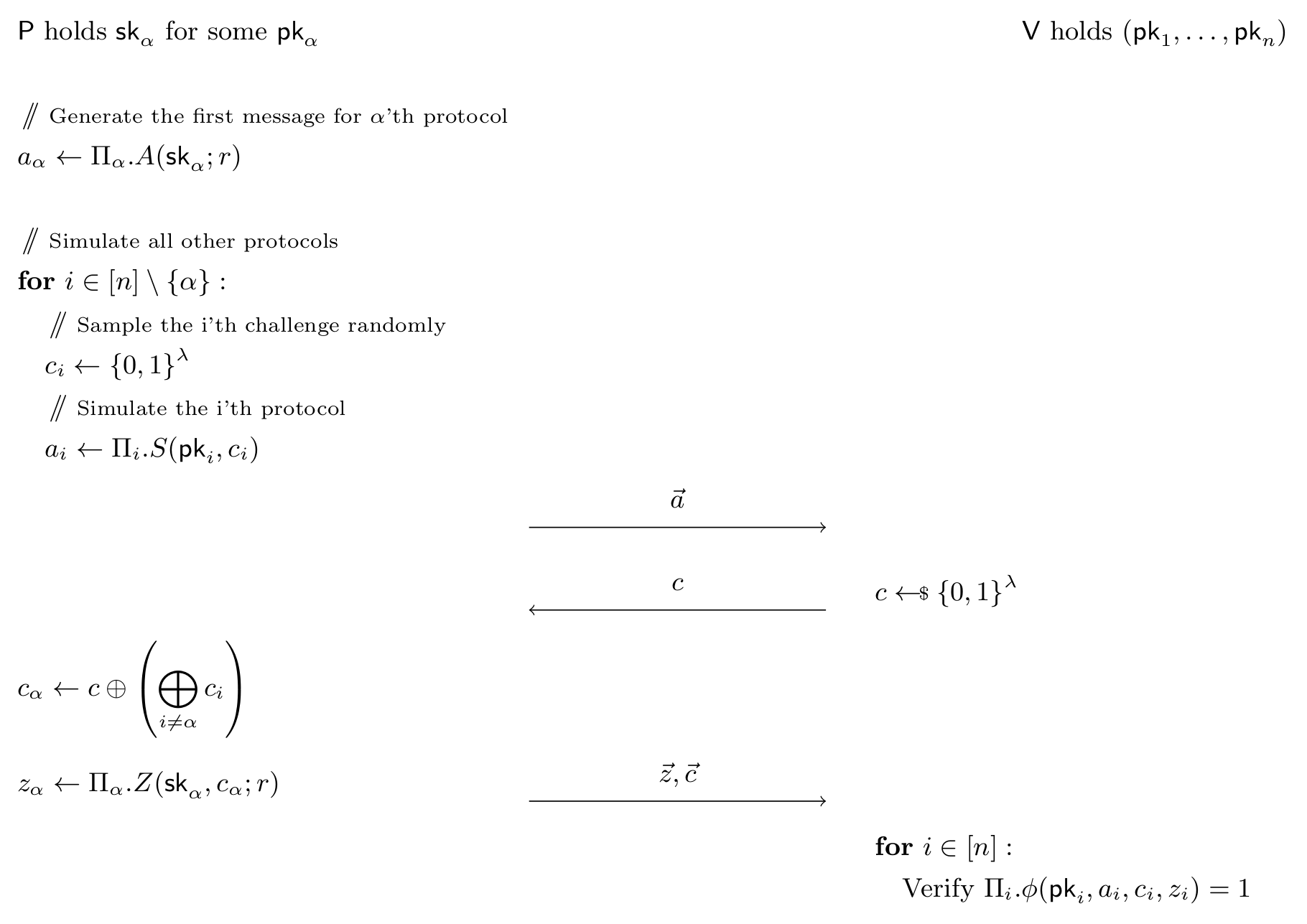
1. Since each \( \Pi_i \) is a \( \Sigma\)-protocol it has a simulator, this simulator outputs \( a_i, z_i \) given the challenge \( c_i \). The prover is going to use this to generate a first-round messages \( a_1, \ldots, a_n \) for all the protocols \( \Pi_1, \ldots, \Pi_n \) as follows:
   • For each \( i \neq \alpha \), the prover can pick \( c_i \) randomly, then run the simulator to obtain \( a_i, z_i \) without knowing \( \sk_i \).
   • For \(i = \alpha \), the prover generates the first message \( a_\alpha \) using he secret key \( \sk_\alpha \) he does know.
   • The prover sends \( a = (a_1, \ldots, a_n) \) to the verifier.
2. The verifier samples \( c \) and sends it to the prover.
3. The prover generates the response as follows.
   • Set the missing challenge \( c_\alpha \) to \( c_\alpha = c \oplus \left(\bigoplus_{i \neq \alpha} c_i\right) \) (where \(\oplus\) is XOR)
   • Generates the missing last-round message \( z_\alpha \) with \( \Pi_\alpha \) using the known secret key \( \sk_\alpha \).
   • Sends \( z = (c_1, \ldots, c_n, z_1, \ldots, z_n) \) to the verifier.

For each \( i \) the verifier checks the validity of each transcript \( a_i, c_i, z_i \) as prescribed in \( \Pi_i \), and additionally that:

\[ c \overset?= \bigoplus_i c_i \]

If everything checks out, they consider the proof valid. Pictorially:

I won’t formally prove that it is sound (it requires the definition of “Special-Soundness”, see the paper for details). The argument below does not quite hold all-the-way-home to a formal proof, but it provides some intuition for why it works:

1. The prover gets to pick the challenges freely for all but one of the protocols.
2. The simulated first round message \( a_i \) for \( i \neq \alpha \), “fixes” the challenges \( c_i \) to which the prover can respond: after all: he did not know a secret key and could answer many different \( c_i \) after sending \( a_i \) – then he could cheat in the original protocol \( \Pi_i \).
3. However, after fixing all \( c_i \) for \( i \neq \alpha \) the distribution of \( c_\alpha \) is uniform over the verifiers challenge \( c \).
4. Therefore the probability of the prover cheating in \( \Pi_\alpha \) remains the same as before applying the compiler.

Overall, he gets to “cheat” (read simulate) in all-but-one of the executions \( \Pi_1, \ldots, \Pi_n \) and the verifier never learns which: from the verifiers point of view they just see \( n \) random strings \( c_1, \ldots, c_n \) subject to \( c = \bigoplus_i c_i \) and \( n \) valid transcripts \( (a_1, c_1, z_1), \) \( \ldots, \) \( (a_n, c_n, z_n) \).

It is elegant (e.g. it requires no additional cryptography) and works for any set of \( \Sigma \)-Protocols. The only potential draw-back of the compiler above is that the proof is now \( n \) times larger. Some people found ways to optimize that for a broad class of protocols.

The next challenge is to get rid of interaction.

Fiat-Shamir Heuristic: From Interactive Protocol to Signatures.

So now we have an interactive proof that the prover knows one of the public keys. But a (ring) signature is non-interactive: you do not need to connect to anyone over the internet to verify the validity of a signature \( \sig \).

Luckily, there is a simple transformation (Fiat-Shamir) which converts 3-round “public-coin protocols” (protocols in which the verifier “has no secrets”) into non-interactive arguments: roughly speaking the idea is to replace the verifiers challenge \( c \) with a hash of the first round message \( a \). Let \( \hash \) be a cryptographic hash function (e.g. SHA512), instead of communicating with the verifier the prover computes a proof like this:

1. Compute the first-round message \( a \) from \( \sk_\alpha \) according to \( \Pi \)
2. Generate the verifiers challenge on your own as: \( c \gets \hash\left(\left(\pk_1, \ldots, \pk_n\right) \ \Vert \ a\right) \)
3. Compute \( z \) according to \( \Pi \) from \( \sk_\alpha, c \).

The proof is \( \sig = (a, z) \), the verifier recomputes the challenge \( c \) from \( a \) and checks the validity of the transcript according to \( \Pi \). Pictorially:

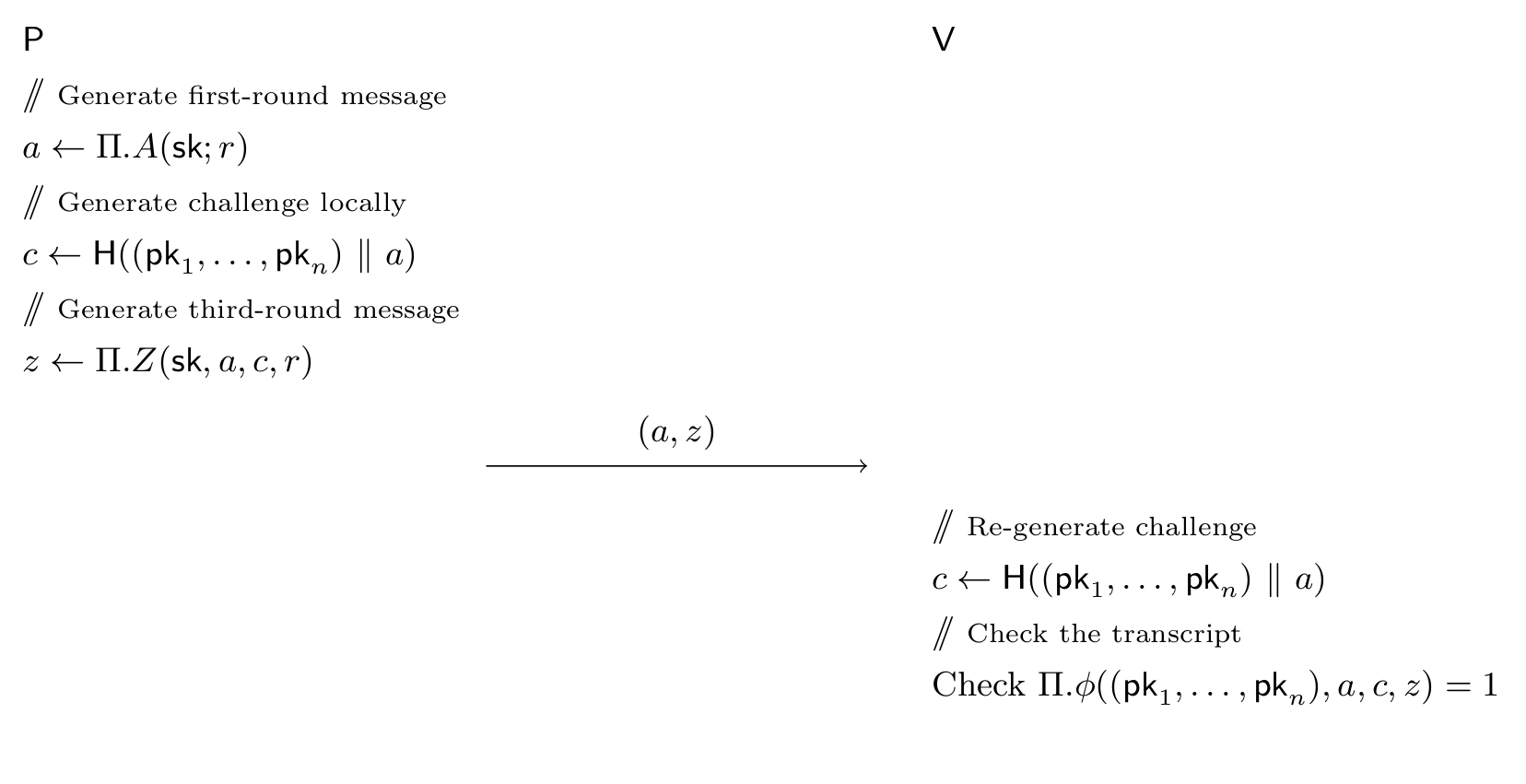
If you want a more in-depth description consider reading the ZKDocs on Fiat-Shamir. Technically, to prove security, this cryptographic hash function must take the form of a “random oracle” – which provable cannot be instantiate by any hash function. Nonetheless this transformation seems to work out fine in practice. See What is the Random Oracle Model and why should you care? by Matthew Green if you are interested in this strange beast.

Before we continue let us briefly cover a few subtleties when applying Fiat-Shamir:

• It is important to include the list of public keys (“the statement”) in the hash, otherwise a malicious prover can generate proofs for rings in which he does not know any private key.
• In the description above we simply concatenate the fields before hashing, however it is important to separate the fields (e.g. by including the length as done in git-ring)

So we now have a proof which is non-interactive, since the verifier can simply recompute \( c \) and check the validity of the transcript, however it is not bound to a message… it is not a signature. Luckily it is very easy to obtain a signature scheme: you simply add the message \( \msg \) you want to sign when computing the hash, the signer generates the signature as follows:

1. Compute the first-round message \( a \) from \( \sk_\alpha \) according to \( \Pi \)
2. Generate the verifiers challenge on your own as: \( c \gets \hash\left(\msg \ \Vert \ \left(\pk_1, \ldots, \pk_n\right) \ \Vert \ a \right) \)
3. Compute \( z \) according to \( \Pi \)

The signature is the transcript, i.e. \( a, z \). The verifier recomputes \( c \) using \( \hash(\cdot) \) from \( \pk_1, \ldots, \pk_n \), \( a \) and \( \msg \), then checks that \( a, c, z \) is an accepting transcript according to the definition of \( \Pi \): running an instance of the protocol \( \Pi \) in which the challenge \( c \) and provers messages \( a, z \) are hard-coded.

Wrap-Up

We constructed heterogeneous ring-signatures by:

• First describing a couple of \(\Sigma\)-protocols (one for each key-type).
• Then applied the CDS compiler to get a protocol enabling the prover to show that they know one-of the secret keys.
• Finally we used the Fiat-Shamir heuristic to convert that protocol into a signature scheme.

That’s the end of the road. If you are interested in how the implementation works take a look at the code.