A walk-through of real-world AES fault injection for dummies on a shoestring budget.
Introduction
In the post we will setup a microcontroller which encrypts using AES with an unknown key, then explore how to recover the full AES key from simply (randomly) glitching the power-supply which will introduce faults in the arithmetic during the computation of AES encryption.
This post is designed to serve as a tutorial and enable the reader to follow along. If you get stuck anywhere (or lack the hardware), just skip the current step and pick up the provided files which will enable you to continue from the next step onwards. To this end there is an associated Github repository which contains the victim code, the attack and visualization scripts as well as the raw samples I collected – which can be used in lieu of setting up the hardware yourself.
The hardware setup in this post is deliberately kept minimal.
We will apply some of the techniques found in the paper “Differential Fault Analysis of the Advanced Encryption Standard using a Single Fault” by Michael Tunstall and Debdeep Mukhopadhyay, however we will not assume that we can precisely control where the fault is injected and instead create a large number of faulty ciphertexts by injecting faults randomly: this is much easier as we do not rely on precise timing.
Prerequisites
If you want to follow along you should make sure you satisfy the prerequisites.
Wetware
I only assume that the reader has:
- The ability to read/write C.
- The ability to read/write Verilog.
- The ability to read/write python3.
- Basic familiarity with finite field arithmetic.
I assume only very minimal familiarity with electronics, since this post is largely aimed at the computer science / “cybersecurity” crowd. The hardware sections in this post can also be skipped entirely.
Hardware
Our target will be the common Atmega328 microcontroller:

To follow along with the hardware section of this post, you will need:
- AVR microcontroller (in a DIP), e.g. Atmega328, acting as the victim.
- FTDI USB-to-Serial device, e.g. FTDI232, for programming and retrieving samples.
- FPGA with YoSys & Nextpnr support. e.g. a board with some variant of an iCE40.
- 10uF capacitor.
- 10kΩ resistor.
- A protoboard.
- Male-Male jumpers to connect it all.
- (potentially) 2N2222 transistor (or similar).
- (optional) 1kΩ resistor.
- (optional) LED, used as indicator.
The transistor will only be needed if the FPGA that you use is incapable of driving the microcontroller directly from an output pin.
I will be using the Atmega328 microcontroller and an old iCE40hx1k FPGA
(circa. 2011) that I had lying around on the Go Board, which means it is driven by a 25MHz clock
and should be sufficiently fast to glitch the Atmega328 running with its internal clock at 8MHz.
If your setup is different you will have to adjust Makefiles accordingly,
but it should be straight forward.
However you must ensure two things:
1. It is important that your microcontroller is not on a board with a large capacitor across the power-rail or very sensitive brown-out detection (for obvious reasons). In particular an Arduino Uno board will not work, however removing the Atmega328PU from an Uno and driving it off an external clock on the protoboard should: you might use the FPGA to generate the clock if you do not have a crystal laying around. The internal brown-out detection on the Atmega328 wont be a problem (the glitch is too short to trigger the time-out).
2. The clock frequency of your FPGA should be significantly higher than the microcontroller, since we will switch power off for a fraction of the execution time of an instruction.
Software
First you should clone the Github repository associated with this tutorial.
We will also need a bunch of open-source tools:
- yosys, for Verilog synthesis.
- nextpnr, for place-and-route.
- avrdude, for flashing the microcontroller.
- pyserial, for collecting samples over the serial port.
- avr-gcc, for compiling C to the microcontroller.
- python3, for collecting samples and analysis.
If you have the Nix package manager you can obtain a shell with yosys and nextpnr by running:
$ nix-shell -p nextpnr yosys
On Debian you can obtain the remainder from the package manager:
$ apt install python3-serial gcc-avr avrdude
In case you are not doing the hardware parts of this tutorial, you only need python.
Programming the victim
I assume that the Atmega328 already has the Arduino bootloader flashed, if not you can find a tutorial on how to flash the bootloader onto an Atmega328 using an Arduino Uno board, go to the “Minimal Circuit (Eliminating the External Clock)” section and follow the steps.
Prepare the setup for programming the microcontroller (howing the FTDI device on the left):
Depending on your LED, you might need an additional 1kΩ resistor between the LED and ground to avoid killing it. Once you map this into 3D space it might look something like this:

Now plug the thing into your computer and make sure it is recognized by Linux (e.g. use lsusb),
then go to the victim/ directory and run:
$ make flash
You may have to adjust the tty (/dev/ttyUSB0 -> /dev/ttyUSB*) for the above to work.
This compiles and flashes the victim program to the AVR microcontroller.
Solution
See victim/victim.c:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78#include <avr/io.h> #include <stdint.h> #include <string.h> #include "aes.h" #define UART_BAUD 9600 char HEX[] = { '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'a', 'b', 'c', 'd', 'e', 'f' }; // secret AES key (pretend you did not see this) uint8_t key[] = { 0x00, 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x0a, 0x0b, 0x0c, 0x0d, 0x0e, 0x0f }; void uart_init(void) { UBRR0 = (F_CPU / (16UL * UART_BAUD)) - 1; UCSR0B = _BV(TXEN0) | _BV(RXEN0); } void uart_putchar(char c) { loop_until_bit_is_set(UCSR0A, UDRE0); UDR0 = c; } void uart_putstr(char *s) { while (*s) { uart_putchar(*s); s++; } } void uart_hex(uint8_t c) { uart_putchar(HEX[c >> 4]); uart_putchar(HEX[c & 0xf]); } __attribute__((optimize("unroll-loops"))) int main (void) { uint8_t pt[AES_BLOCKSIZE]; aes_expanded_key_t ekey; // setup serial uart_init(); // set pin 5 of PORTB for output DDRB |= _BV(DDB5); // set pin 5 high to turn led on */ PORTB |= _BV(PORTB5); // expand AES key aes_expand(&ekey, key); // repeatedly encrypt same plaintext uart_putstr("\n\r"); while(1) { // pt <- 0^16 memset(pt, 0, sizeof pt); // pt <- AES128(key, 0^B) aes_encrypt(pt, &ekey); // print(pt) for (uint8_t i = 0; i < sizeof pt; i++) uart_hex(pt[i]); uart_putchar('\n'); uart_putchar('\r'); } }
The program causes the microcontroller to repeatedly output the hexadecimal encoding of \( \texttt{AES-128}(k, 0^{16}) \), the encryption of the all zero plaintext, on the serial port. e.g. using miniterm.py which you got along PySerial, you should observe:
--- Available ports:
--- 1: /dev/ttyUSB0 'FT232R USB UART'
--- Enter port index or full name: 1
--- Miniterm on /dev/ttyUSB0 9600,8,N,1 ---
--- Quit: Ctrl+] | Menu: Ctrl+T | Help: Ctrl+T followed by Ctrl+H ---
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
c6a13b37878f5b826f4f8162a1c8d879
...
Going on into infinity…
Inducing Glitches
But having a microcontroller which consistently does the right thing is not
exactly the goal of this post.
In this section we will try to make the microcontroller occasionally do the wrong thing:
to make a mistake somewhere in the call to aes_encrypt.
Our first task is to control the power of microcontroller from the FPGA,
so start by removing the jumper between Vout on the FTDI and the power rail on the protoboard.
Depending on whether the output pins of your FPGA delivers sufficient power
you may/may not have to use a transistor.
We consider both these possibilities.
In my case I will power the Atmega328 directly from the PMOD connector on the Go Board,
by wiring one of the ground pins from the PMOD connector to ground on the protoboard
and the 4th pin (M4) to power.
Setup powering the microcontroller directly from the FPGA.
Which looks approximately like this when mapped to the real world:

Setup powering the microcontroller from an external power source.
Which looks approximately like this when mapped to the real world:

These setups lets you easily switch back/forth between programming the microcontroller and glitching if you want to experiment further on your own e.g. try to simply glitch a comparison to bypass authentication.
Exercise.Write a Verilog program which executes the following procedure on the FPGA:
- Switch power on for 1 second (allowing the microcontroller to start up).
- Then 5000 times:
- Switch power off for < 1 / 8 000 000 of a second
- Switch power on for 1 / 2 000 of a second
- Switch power off for 1 second (shutting off the microcontroller).
- Go to the first step.
There is a
Makefilein attacker/ which should aide in the process of flashing the program to the FPGA if you are using the Go Board. If you are using another iCE40 FPGA the modifications should be straight-forward. You might want to play around with the length of the glitches and the duration between them. I switch power off for 1 / 25 000 000 of a second.You will know that you have succeeded by connecting to the serial port (like before) and observing that the ciphertexts occasionally deviates from the correct encryption observed earlier. Here are some successful glitches (from the reference solution). The deviating ciphertexts has been marked:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 5b39c343e831f4b4787dac01a0a78b69 ff0fe5db6edd48de705bb37837e2fd44 c6a13b37878f5b826f4f8162a1c8d879 c6a13bbe878f5b826f4f816233c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 fb568222c589024cec16ee90182f6d53 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a1783787405b82ee4f8162a1c8d831 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879 c6a13b37878f5b826f4f8162a1c8d879Solution (Click to Expand)
See attacker/glitch.v:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77// chip: ice40hx1k // board: go-board parameter CLK_HZ = 25000000; // 25 MHz parameter CONTROL_HZ = 8000000; // 8 MHz parameter RESET = 2'b00; // power off parameter POWER = 2'b01; // power on parameter GLITCH = 2'b10; // do the glitch parameter WAIT = 2'b11; // wait for boot parameter GLITCHES = 5000; // glitch 5000 times before reset parameter WAIT_LEN = CLK_HZ; parameter RESET_LEN = CLK_HZ; parameter POWER_LEN = CLK_HZ / 2000; parameter GLITCH_LEN = 1; module Top( input CLK, output reg LED1, output reg LED2, output reg LED3, output reg LED4, output reg PMOD4, ); reg [1:0] state = RESET; reg [$clog2(CLK_HZ) + 5:0] cnt; reg [$clog2(GLITCHES):0] glitches; always @(posedge CLK) begin LED1 <= 0; LED2 <= 0; LED3 <= 0; LED4 <= 0; cnt <= cnt + 1; case (state) RESET : begin LED1 <= 1; PMOD4 <= 0; if (cnt > RESET_LEN) begin cnt <= 0; state <= WAIT; end end WAIT : begin LED2 <= 1; PMOD4 <= 1; if (cnt > WAIT_LEN) begin cnt <= 0; state <= GLITCH; glitches <= 0; end end POWER : begin LED3 <= 1; PMOD4 <= 1; if (cnt > POWER_LEN) begin cnt <= 0; state <= GLITCH; end end GLITCH : begin PMOD4 <= 0; if (cnt > GLITCH_LEN) begin cnt <= 0; state <= POWER; glitches <= glitches + 1; end if (glitches > GLITCHES) begin cnt <= 0; state <= RESET; end end endcase end endmodule
Sitting around and manually collecting the divating ciphertext samples is silly, especially since we just automated the glitching part…
So automate this part as well:
Exercise.Write a python script to automatically collect the ciphertexts from the serial port using PySerial, remove duplicates and save them to a file.Solution (Click to Expand)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39#!/usr/bin/env python3 import sys import serial import binascii ser = serial.Serial(sys.argv[1]) try: with open(sys.argv[2], 'r') as f: cts = map(str.strip, f.readlines()) cts = [binascii.unhexlify(x) for x in cts] cts = set(cts) except IOError: cts = set([]) out = open(sys.argv[2], 'a') print('Samples:', len(cts)) print('Collecting samples from:', ser.name) line = b'' while 1: line += ser.read() if b'\n' in line: line = line.strip() try: line = binascii.unhexlify(line) if len(line) == 16: print('Ciphertext:', line.hex()) if line not in cts: print('New:', line.hex()) out.write(line.hex() + '\n') out.flush() cts.add(line) except binascii.Error: pass line = b'' ser.close()
Let it run for a while until you have a file with a few hundred distinct ciphertexts. I was able to successfully mount the attack with as little as ~ 20 samples, but collect a few more for good measure.
If you were unable to complete this section: use the provided attacker/samples.txt which I collected from the setup shown in this section and which will enable you to follow along in the cryptanalysis part of this post.
AES(-128) encryption
In order to make sense of the faulty ciphertexts we will need to understand the internals of AES.
The AES wikipedia article covers most of the content in this section (from which I also pilfered the illustrations), however I include it here for completeness. If you prefer stick figures then there is even A Stick Figure Guide to the AES. For those who prefer C, it might be easier to read my didactic implementation of AES-128 which we are attacking in this post victim/aes.c victim/aes.h (\(\approx\) 150 lines) included in the git repository. Hopefully by the end of this section you will realize that AES has a very intuitive structure.
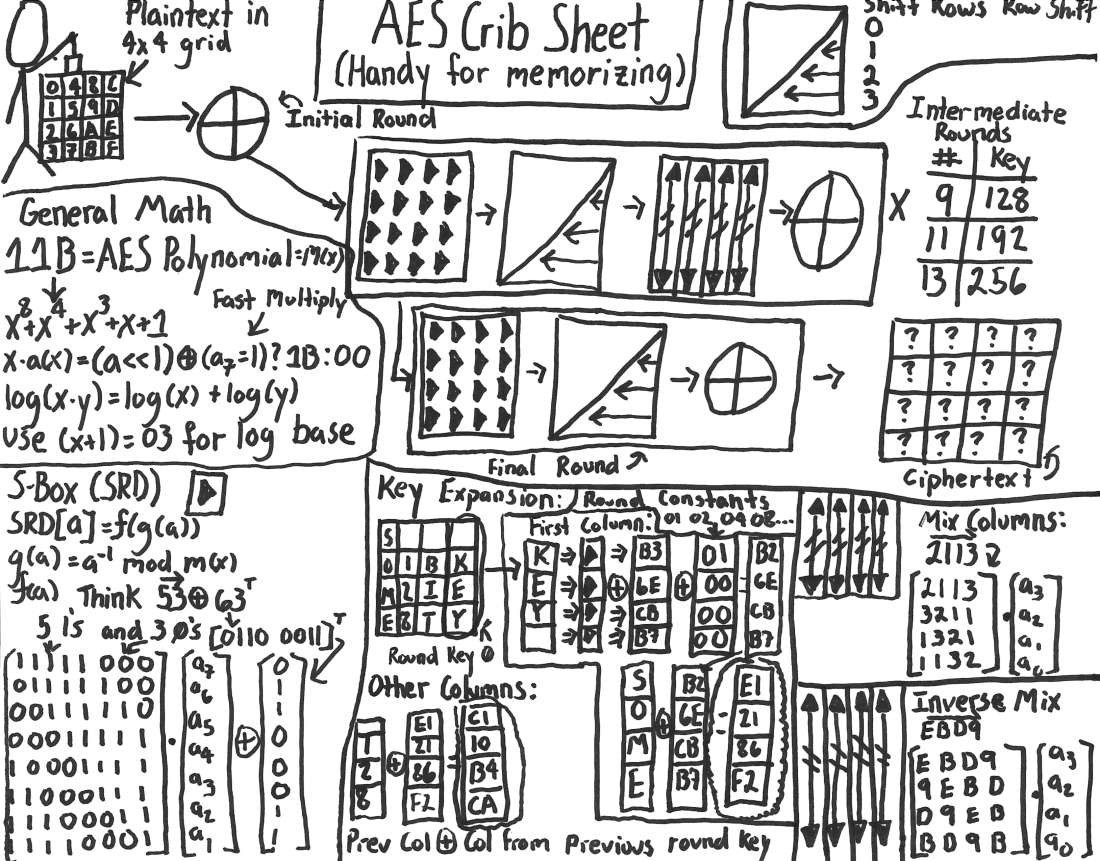
Bytes are interpreted as elements of \( \mathbb{F}_{2^8} = \mathbb{F}_2[X] / (X^8+X^4+X^3+X+1) \) in the straight-forward way, by mapping the bits to the coefficients of a canonical representative, where the least significant bit is the constant term. For those new to this, see the crash-course below.
Crash-course on the AES extension field (click to expand)
Operations in AES is done over the field \( \mathbb{F}_{2^8} = \mathbb{F}_2[X] / (X^8+X^4+X^3+X+1) \), i.e. the quotient group formed by taking univariate polynomials with coefficients in \( \mathbb{F}_2 \) modulo the irreducible polynomial \(X^8 + X^4 + X^3 + X + 1\). In other words adding/subtracting multiples of \( X^8 + X^4 + X^3 + X + 1 \), like \( X^9 + X^5 + X^3 + X^2 + 1 = \) \( (X + 1) (X^8 + X^4 + X^3 + X + 1) \equiv \) \( 0 \mod X^8 + X^4 + X^3 + X + 1 \) each represent the same element, analogous to arithmetic modulo a natural number (i.e. \( \mathbb{Z}_n \)). The elements of \( \mathbb{F}_{2^8} \) can be represented as bytes in a natural way:
Representation: Given a byte \( B = \sum_{i = 0}^{7} b_i \cdot 2^i \), it is interpreted as a polynomial \( p_{B}(X) = \sum_{i = 0}^{7} b_i \cdot X^i \); a canonical representative for the coset.
Addition: Addition of elements in an extension field is simply addition of polynomials: addition is done pairwise on the coefficients for every power. Since the group has characteristic 2, addition and subtraction in the group is the same and the common nomenclature for this sophisticated operation is “xor of bytes”, e.g. \[ \texttt{0x54} = \texttt{01010100}_{2} =_{repr} X^6 + X^4 + X^2 \] \[ \texttt{0x64} = \texttt{01100100}_{2} =_{repr} X^6 + X^5 + X^2 \] \[ \texttt{0x30} = \texttt{0x54} \oplus \texttt{0x64} = \texttt{00110000}_{2} \] \[ \texttt{0x30} =_{repr} (X^6 + X^4 + X^2) + (X^6 + X^5 + X^2) = (2 \cdot X^6) + X^5 + X^4 + (2 \cdot X^2) \] \[ \texttt{0x30} =_{repr} (0 \cdot X^6) + X^5 + X^4 + (0 \cdot X^2) = X^5 + X^4 \]
Multiplication: Multiplication of elements in an extension field is likewise multiplication of polynomials, however unlike addition a reduction might be required: \[ \texttt{0x54} = \texttt{01010100}_{2} =_{repr} X^6 + X^4 + X^2 \] \[ \texttt{0x64} = \texttt{01100100}_{2} =_{repr} X^6 + X^5 + X^2 \] \[ R(X) = (X^6 + X^4 + X^2) \cdot (X^6 + X^5 + X^2) = X^{12} + X^{11} + X^{10} + X^9 + 2 \cdot X^8 + X^7 + X^6 + X^4 \] Then we separate out all the multiples of \( X^8 + X^4 + X^3 + 1 \): \[ R(X) = (-X^7 - X^6 - 2 X^5 - 2 \cdot X^4 - 2 \cdot X^3 - X^2 - X - 1) + (X^8 + X^4 + X^3 + 1) (X^4 + X^3 + X^2 + X + 1) \] Since \( 2 \equiv 0\mod 2 \), \( - 1 \equiv 1\mod 2 \), the final reduced canonical representative is: \[ R(X) \equiv X^7 + X^6 + X^2 + X + 1 \mod X^8 + X^4 + X^3 + 1 \]
This can be efficiently implemented using a variant of modular long multiplication on the byte/integer representations of the elements. The pseudocode for this procedure look as follows:
func mult(a, b) {
r = 0
p = 0b100011011 // (X^8+X^4+X^3+X+1)
while a > 0:
// add if the constant term is set
if a & 1 == 1:
r ^= b
a >>= 1
// multiply by "X"
b <<= 1
if b >> 8 == 1:
b ^= p
return r
}
The state of AES consists of 16 field elements of \(\mathbb{F}_{2^8}\), which conveniently can be represented as bytes: A “flat” plaintext/ciphertext array of 16 bytes \( a_{0,0}, a_{1,0}, a_{2,0}, a_{3,0}, \) \( a_{0,1}, a_{1,1}, a_{2,1}, a_{3,1}, \) \( a_{0,2}, a_{1,2}, a_{2,2}, a_{3,2}, \) \( a_{0,3}, a_{1,3}, a_{2,3}, a_{3,3} \) is interpreted as a 4x4 matrix of \(\mathbb{F}_{2^8})\) elements column-by-column:
\[ \begin{bmatrix}a_{0, 0} & a_{0,1} & a_{0,2} & a_{0, 3} \\ a_{1,0} & a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,0} & a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,0} & a_{3,1} & a_{3,2} & a_{3,3} \end{bmatrix} \in M_{4}(\mathbb{F}_{2^8}) \]
There are 4 different transformations applied to the state matrix in AES:
SubBytes
SubBytes replaces every element in the state by applying a permutation (the S-box).
We will revisit the exact value of the S-box later, when we extract key-material from the samples.
SubBytes is the only non-linear (over \(\mathbb{F}_{2^8} \)) operation applied in AES.
Note: The AES S-Box is carefully chosen to enable cheap hardware implementation (without lookup tables) while providing excellent protection against linear and differential cryptanalysis.
ShiftRows
ShiftRows rotates each row by a different amount,
this moves an entry from every column to every other
and provides “mixing” across columns:
Note: ShiftRows can be implemented at no cost,
since it is merely a relabeling of the elements in the state.
MixColumns
MixColumns applies an MDS (Maximum Distance Separable) matrix to every column independently.
MixColumns is the only operation which does not operate on a “byte-by-byte” basis
and provides “diffusion” within each column:
Note: Since the matrix is MDS any single element change to the input column affects every element of the new column. The MDS property is integral to the “wide-trail strategy” which protects AES against linear and differential cryptanalysis.
AddRoundKey
AddRoundKey adds a secret round-key matrix to the state matrix (addition of matrices):
Note: We will revisit how the round-keys are generated later.
Rounds
AES-128 then operates by applying the transformation above in order for 10 rounds:
- Initial round:
AddRoundKey
- For 9 rounds:
SubBytesShiftRowsMixColumnsAddRoundKey
- Final round:
SubBytesShiftRowsAddRoundKey
Finally the state matrix is again interpreted as a flat array (column-by-column) of bytes,
which forms the ciphertext.
Since both MixColumns and AddRoundKey are linear in \(\mathbb{F}_{2^8}\), the omission of MixColumns
in the final round has no effect on security: let \( a_i \) be a row of the state then MixColumns followed by AddRoundKey
can be expressed as \(b_i = C(a_i) + k_i^{r} \),
given such a ciphertext the adversary can simply compute
\(
C^{-1}(a_i)
\)
\(
= C^{-1}(C(a_i)) + C^{-1}(k_i^{r})
\)
\(
= a_i + C^{-1}(k_i^{r})\)
which gets rid of the diffusion induced by the final MixColumns.
Now you are ready to quiz yourself on AES:
Exercise.If a single element in the state is changed at the start of a round, how many elements are changed by the end of the round?Solution (Click to Expand)
4 elements are changed at the end of the round:
SubBytespreserves the difference,ShiftRowspreserves the difference,MixColumnscauses all elements in the column to change (since it is multiplication by an MDS matrix),AddRoundKeypreserves the 4 resulting differences.
Exercise.How many rounds does “full diffusion” take in AES? i.e. if a single byte is changed in the state, how many rounds are required before this causes every byte in the state to change?Solution (Click to Expand)
Full diffusion occurs within 2 rounds (as per the previous exercise).
Exercise.Explain why AES encryption starts withAddRoundKey.Solution (Click to Expand)
Otherwise the firstSubBytes,ShiftRowsandMixColumnscan be trivially inverted.
Exercise.AES becomes trivially breakable if we remove any of the transformations, regardless of how they are composed or how many rounds we apply. Explain why.Solution (Click to Expand)
- Omitting
SubBytes: AES becomes completely affine: every ciphertext c_i can be computed as c_i = M x + k for some M and k. Which enables the adversary to recover the key by Gaussian elimination.- Omitting
ShiftRows: AES decomposes into 4 parallel 32-bit blockciphers. Which enables you to construct the full codebook by encryption only \(2^{32}\) plaintexts.- Omitting
MixColumns: AES decomposes into a 16 parallel instances of an 8-bit blockcipher. Which enables you to construct the full codebook by encrypting only \(2^8\) plaintexts.- Omitting
AddRoundKey: Clearly broken.
Recovering the last round key
With our new found knowledge of AES, we start by getting a better grasp of the data we just collected, which also serves as a sanity check for our collection process. If you skipped the hardware section earlier use the samples from attacker/samples.txt for the remainder of this post.
Understanding the data
Note: The Hamming distance is simply the number of differing symbols between two strings, e.g. \(D_{H}(01011, 10111) = 3\), below each symbol is an element of \( \mathbb{F}_{2^8} \) or you know: a byte. Hence each string (ciphertext) contains 16 symbols and we count the number of differing bytes.
If you plot a histogram (e.g. using attacker/hist.py) of the Hamming distance between each faulty ciphertext and the correct ciphertext, you should get something like the following plot:
The shape of this distribution reveals something about the structure of AES that we learned earlier (in an exercise) and tells us where the fault for a particular faulty ciphertext was induced. This will allow us to filter out the faults that we will use for our attack. We will focus on the spikes at 1, 2, 4, 8, 15 and 16:
Distance | Justification |
|---|---|
| 1 | A difference of 1 byte is caused when the fault is introduced in the final round, during either SubBytes, ShiftRows or AddRoundKey. The last round omits MixColumns and therefore operates entirely on a byte-by-byte basis.Another plausible cause of 1 symbol errors is the hexadecimal conversion code in the victim program. |
| 2 | A difference of 2 bytes is caused by 2 faults in the last round. |
| 4 | A difference of 4 bytes indicates that a single fault is induced before/during MixColumns in round 9, but after MixColumns in round 8. As noted in an earlier exercise this causes 4 elements of the state to change in round 10, which omits the MixColumns step and hence operates entirely element wise. |
| 8 | A difference of 8 bytes indicates 2 faults in the before/during MixColumns in round 9, but after MixColumns in round 8. |
| 15 & 16 | A completely random looking ciphertext indicates that the fault is induced in an earlier round, which causes the fault to diffuse (in 2 rounds, as noted in an earlier exercise). The number of entries with a Hamming distance of 15 bytes is very close the statical expectation:\( 144 \approx (2340 + 144) \cdot \frac{1}{256} \cdot \Big(\frac{255}{256}\Big)^{15} \cdot { 16 \choose 1 } = 145.8260\) i.e. what we would expect if we sampled these ciphertexts uniformly at random. |
Differential faults on AES
To get started lets consider the propagation of a single fault in the 9th round of AES, just before the final MixColumns (recall that the 10th round omits MixColumns).
The remaining section of the cipher causes the fault to propagate as follows:
MixColumns(round 9) causes the single difference to be propagate to the entire column.AddRoundKey(round 9) is a bijection and hence all 4 differences are preserved.SubBytes(round 10) is a bijection and hence all 4 differences are preserved.ShiftRows(round 10) is applied which permutes the elements in each.AddRoundKey(round 10) is a bijection and hence all 4 differences are preserved.
The propagation of the fault is illustrated below (ignoring the element-wise bijections):
Hence a fault introduced in any element of the first column, causes a difference to every element in the column after MixColumns,
then ShiftRows is applied which permutes the indexes of the first column [1, 2, 3, 4] to [1, 14, 11, 8] respectively.
Therefore we get a non-zero difference in the 1st, 8th, 11th and 14th byte of the faulty ciphertext
as seen in the illustration above.
Exercise.Since the state consists of 4 columns, if a single fault is induced prior to the finalMixColumnsapplication there are 4 different and disjoint (ordered) list of indexes in which the faulty ciphertext can differ from the correct ciphertext. The first such list ([1, 14, 11, 8]) is given above, compute the remaining 3 lists.Solution (Click to Expand)
- 1st column: [1, 2, 3, 4]
--ShiftRows->[ 1, 14, 11, 8 ]- 2nd column: [5, 6, 7, 8]
--ShiftRows-->[ 5, 2, 12, 15 ]- 3rd column: [9, 10, 11, 12]
--ShiftRows-->[9, 6, 3, 16]- 4th column: [13, 14, 15, 16]
--ShiftRows-->[13, 10, 7, 4]
Exercise.Is this observation consistent with the samples you collected?
Compare the indexes of the faulty ciphertexts with a Hamming distance of 4 from the correct ciphertext.
Okay, so given such a scenario how can be begin to recover key material? Key-recovery in symmetric cryptography often involves making a guess for some part of the key-material, then using this guess to partially encrypt/decrypt and test a relation part-way inside the cipher which will be satisfied if our guess was correct. Particularly for those familiar with the key recovery procedure used in differential cryptanalysis the method applied here bares a striking resemblance: Like differential cryptanalysis we will guess part of the last round key, then attempt partial decryption and use whether the differential relation is satisfied to validate/reject our candidate.
Assume for now that we know in which of the 4 columns a fault is introduced and the difference \( \delta \neq \mathbf{0} \) introduced by the fault, a vector \( \delta \in (\mathbb{F}_{2^8})^4 \), i.e. the faulty value is \( y’ = y + \delta \) where \( y \) (unknown) was the original correct value. If we know \( \delta \) we can recover candidates for 4 bytes of the last round key as follows:
Compute \( \Delta = C \ \delta \) corresponding to the difference introduced by the fault after the
MixColumnstransformation, i.e. sinceMixColumnsis linear: \( \ C \ y’ = C (\delta + y) = C \ \delta + C \ y \)Given the list of faulty indexes for the row \( [ i_{1}, \ldots, i_{4} ] = I_{row} \). For every \(j \in [1, 4]\), obtain candidates \( K_j \) for the \(i_j\)’th byte of the last round key as follows:
Let \( x_{i_j} \) be the \( i_j \)’th element from the correct ciphertext and let \( x_{i_j}’ \) be the \( i_j \)’th element of the faulty ciphertext. Guess the corresponding byte of the last round key \(k^{10}_{i_j}\), then do partial decryption of the last round by computing \( z_{j} = S^{-1}(x_{i_j} - k^{10}_{i_j}) \), \( z_{j}’ = S^{-1}(x_{i_j}’ - k^{10}_{i_j}) \), compute the difference \( \rho_j = z’_j - z_j \). Observe that the key-addition in round 9 does not affect the difference, since \( \rho_j = (z’_{j} - e) - (z_{j} - e) \) for any \( e \).
If our guess for \( k^{10}_{i_j} \) was correct then \( \rho_{j} = \Delta_{j} \). Thus if \( \rho_{i} = \Delta_j \), we add our guess for \( k^{10}_{i_j}\) to the set \( K_{j} \) of candidates for the \(i_j\)’th byte of the last roundkey.
Compute the product \(K_1 \times K_2 \times K_3 \times K_4 \) to obtain a set of candidates for 32-bits of the last round key.
Example.Assume that the fault introduces a difference \( \delta = \texttt{0x85} \) in the first entry (first row) in the first column. The differences in the column after applying
MixColumnsbecomes: \[ \Delta = C \begin{bmatrix}
\delta
\\ 0
\\ 0
\\ 0
\end{bmatrix} = \begin{bmatrix} 2 & 3 & 1 & 1 \\
1 & 2 & 3 & 1 \\
1 & 1 & 2 & 3 \\
3 & 1 & 1 & 2 \end{bmatrix} \begin{bmatrix}
\delta
\\ 0
\\ 0
\\ 0
\end{bmatrix} = \begin{bmatrix} 2 \delta \\
\delta \\
\delta \\
3 \delta
\end{bmatrix} = \begin{bmatrix} \texttt{0x11} \\
\texttt{0x85} \\
\texttt{0x85} \\
\texttt{0x94}
\end{bmatrix} \] As noted earlier, after applyingShiftRowsthe column is mapped to the indexes \( I = [ 1, 14, 11, 8] \). We for each index \(i_j \in I\) we execute the procedure. i.e.
- For \( i_1 = 1 \), try every possible value for \( k^{10}_{1} \), compute \( \rho_1 = S^{-1}(x_1 - k^{10}_1) - S^{-1}(x’_1 - k^{10}_1) \), if \( \rho_1 = \Delta_{1} = 2 \delta = \texttt{0x11} \) then \( k^{10}_1 \) is a candidate for the first byte of the last round key.
- For \( i_2 = 14 \), try every possible value for \( k^{10}_{14} \), compute \( \rho_2 = S^{-1}(x_{14} - k^{10}_{14}) - S^{-1}(x’_{14} - k^{10}_{14}) \), if \( \rho_2 = \Delta_{2} = \delta = \texttt{0x85} \) then \( k^{10}_{14} \) is a candidate for the second byte of the last round key.
- For \( i_3 = 11 \), try every possible value for \( k^{10}_{11} \), compute \( \rho_3 = S^{-1}(x_{11} - k^{10}_{11}) - S^{-1}(x’_{11} - k^{10}_{11}) \), if \( \rho_3 = \Delta_{3} = \delta = \texttt{0x85} \) then \( k^{10}_{11} \) is a candidate for the third byte of the last round key.
- For \( i_4 = 8 \), try every possible value for \( k^{10}_{8} \), compute \( \rho_4 = S^{-1}(x_{11} - k^{10}_{8}) - S^{-1}(x’_{8} - k^{10}_{8}) \), if \( \rho_4 = \Delta_{4} = 3 \delta = \texttt{0x94} \) then \( k^{10}_{8} \) is a candidate for the fourth byte of the last round key.
After recovering the candidates for every \( i_j \) under the same \( \delta = \texttt{0x85} \) you then compute the direct product of the sets to obtain every 32-bit partial key-candidate (for the indexes of the full round key in the set I). In particular if no \( k^{10}_{i_j} \) satisfies \( \rho_{j} = \Delta_{j} \) for some \(j\), then \( \delta_i = \texttt{0x85} \) is an “impossible differential” and there exists no key consistent with the assumption \( \delta = \texttt{0x85} \).
In other words, given a vector of differentials after MixColumns “D” (\(\Delta\) in the example above)
and list of indexes after ShiftRows “I” (I in the example above),
pseudocode for key-recovery looks as follows:
func possible_keys(D, I, ct, ct') {
// recover candidates for each byte
ks = [{}, {}, {}, {}]
for i in [1, ..., 4]:
for k in [0, ..., 0x100]:
x = ct[I[i]]
x' = ct'[I[i]]
d = Sinv[x xor k] xor Sinv[x' xor k]
if d == D[i]:
ks[i].add(k)
// compute 32-bit partial keys
return product(ks)
}
Exercise.Implement the program above in python.
You will need the concrete AES sbox (and to compute its inverse yourself):
sbox = [ 0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76, 0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0, 0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15, 0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75, 0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84, 0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF, 0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8, 0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2, 0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73, 0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB, 0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79, 0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08, 0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A, 0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E, 0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF, 0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16 ]Solution (Click to Expand)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18import itertools def solve(xA, xB, D): ks = [] for k in range(0x100): if D == sboxI[xA ^ k] ^ sboxI[xB ^ k]: ks.append(k) assert len(ks) in (0, 2, 4) return ks def possible_keys(D, I, ct_correct, ct_fault) ks = [[], [], [], []] for j, i in enumerate(I): ks[j] = solve(ct_correct[i], ct_fault[i], D[j]) if len(ks[j]) == 0: break return itertools.product(*ks)
We are also going to need some code to actually calculate “D” for every possible single element fault in any position of a column. From the example earlier it should be clear enough how to do this.
Exercise.Write code to compute “D” based on the row and difference of the fault. Remember that multiplication (mult) is not in the integers but in \( \mathbb{F}_2[X] / (X^8+X^4+X^3+X+1) \). You can use the example earlier to test your code.Solution (Click to Expand)
Excerpt from attacker/extract.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33def mult(a, b): assert 0x100 > a >= 0 assert 0x100 > b >= 0 r = 0 p = 0b100011011 while b: if b & 1: r ^= a a <<= 1 b >>= 1 if a >> 8: a ^= p return r def mix_column(v): assert len(v) == 4 r1 = mult(2, v[0]) ^ mult(3, v[1]) ^ v[2] ^ v[3] r2 = v[0] ^ mult(2, v[1]) ^ mult(3, v[2]) ^ v[3] r3 = v[0] ^ v[1] ^ mult(2, v[2]) ^ mult(3, v[3]) r4 = mult(3, v[0]) ^ v[1] ^ v[2] ^ mult(2, v[3]) return (r1, r2, r3, r4) def mix_fault(d, row): col = [0, 0, 0, 0] col[row] = d return mix_column(col)
So how do we figure out which fault is induced in which row and column?
The simple answer is that we do not: for each of the 4 sets of indexes “I”, we iterate over every faulty ciphertext which differs from the correct ciphertext at every index in “I”. For each such ciphertext we try every possible “D”, then keep a count of how many times we see any particular key candidate. If we guess correctly then the counter for the correct key will be increased, if not we assume that the erroneous key candidate will be sampled uniformly at random.
Hence across multiple samples the correct key will have a significantly higher frequency than any other candidate: it will emerge consistently whenever we guess correctly, while the erroneous candidates will be distributed uniformly. In the cases where faults are injected very early in the cipher, every key candidate will be part of “the noise floor” of keys from erroneous guesses. This process is very similar to simple key-recovery in differential/linear cryptanalysis, where you can keep a counter for every candidate, which is then increased for every ciphertext & plaintext pair for which the linear/differential characteristic is satisfied.
Exercise.Implement the full round key recovery program. The program should:
- Load the samples (from
samples.txt) and the correct ciphertext.- Compute a list of every possible \(\Delta\) (\( 255 \times 4 \) elements).
- Compute a list of every possible \(I\) (4 elements).
- Initialize \(\text{KEY} = 0^{16} \).
- For every \(I\):
- Initialize the map \(\text{cnt} = \emptyset\).
- For every sample:
- Compute the set \( \mathcal{I} \) of indexes in which the correct ciphertext and the sample differs. If \( I \not\subseteq \mathcal{I} \), then ignore the sample.
- Otherwise, use the key recovery procedure earlier to recover the key candidates \(K\). For every \( k \in K\), increment \( \text{cnt}[k] \) by one.
- Pick the value \(k\) for which \(\text{cnt}[k]\) which is maximal and update the full guess for the last round key: For every \( j \in [1,4] \) set \( \text{KEY}_{I_j} = k_j \).
- Output \(\text{KEY}\).
Solution (Click to Expand)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187#!/usr/bin/env python3 import sys import binascii import itertools import collections sbox = [ 0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76, 0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0, 0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15, 0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75, 0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84, 0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF, 0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8, 0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2, 0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73, 0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB, 0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79, 0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08, 0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A, 0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E, 0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF, 0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16 ] # shift row permutation on indexes shift_rows = [ 0, 13, 10, 7, 4, 1, 14, 11, 8, 5, 2, 15, 12, 9, 6, 3, ] # indexes for every column cols = [ (0, 1, 2, 3), (4, 5, 6, 7), (8, 9, 10, 11), (12, 13, 14, 15) ] def inv_perm(perm): inv = [0] * len(perm) for i in range(len(perm)): inv[perm[i]] = i return inv sboxI = inv_perm(sbox) def mult(a, b): assert 0x100 > a >= 0 assert 0x100 > b >= 0 r = 0 p = 0b100011011 while b: if b & 1: r ^= a a <<= 1 b >>= 1 if a >> 8: a ^= p return r def mix_column(v): assert len(v) == 4 r1 = mult(2, v[0]) ^ mult(3, v[1]) ^ v[2] ^ v[3] r2 = v[0] ^ mult(2, v[1]) ^ mult(3, v[2]) ^ v[3] r3 = v[0] ^ v[1] ^ mult(2, v[2]) ^ mult(3, v[3]) r4 = mult(3, v[0]) ^ v[1] ^ v[2] ^ mult(2, v[3]) return (r1, r2, r3, r4) def mix_fault(d, row): col = [0, 0, 0, 0] col[row] = d return mix_column(col) def recover(ct_correct, ct_fault, I, K): assert len(I) == 4 assert len(ct_correct) == len(ct_fault) == 16 def solve(xA, xB, D): ks = [] for k in range(0x100): if D == sboxI[xA ^ k] ^ sboxI[xB ^ k]: ks.append(k) assert len(ks) in (0, 2, 4) return ks for row in range(4): # guess the row of the fault for d in range(1, 0x100): # guess the difference D = mix_fault(d, row) # calculate candiates for each byte ks = [[], [], [], []] for j, i in enumerate(I): ks[j] = solve(ct_correct[i], ct_fault[i], D[j]) if len(ks[j]) == 0: break # expand the cross product to get full 32-bit keys for k in itertools.product(*ks): K[k] += 1 def diff(s1, s2): idx = set([]) for i in range(len(s1)): if s1[i] != s2[i]: idx.add(i) return frozenset(idx) if __name__ == '__main__': # sample file with open(sys.argv[1], 'r') as f: samples = map(str.strip, f.readlines()) samples = [binascii.unhexlify(s) for s in samples] # correct ciphertext correct = binascii.unhexlify(sys.argv[2]) # optional threshold try: threshold = int(sys.argv[3]) except IndexError: threshold = None # group ciphertext by faulty indexes Is = [tuple([shift_rows[v] for v in col]) for col in cols] groups = { I: [] for I in Is} for sample in samples: df = diff(sample, correct) for I in Is: if all([i in df for i in I]): groups[I].append(sample) # extract from every group of faulty indexes KEY = [None] * 16 for I in Is: print('I : %14s, ciphertexts: %d' % (I, len(groups[I]))) # find the most seen 32-bit key candidates K = collections.Counter() for i, sample in enumerate(groups[I]): recover(correct, sample, I, K) # print status show = ''.join(['%02x' % v if v else '??' for v in KEY]) print('Key: %s, Sample %d / %d, Cand: %d, Top: %s' % (show, i, len(groups[I]), len(K), K.most_common(2))) # check optional threshold try: _, cnt = K.most_common(1)[0] if cnt >= threshold: break except: pass # fill in the full round key with the recovered 32-bits key, _ = K.most_common(1)[0] for j, i in enumerate(I): assert KEY[i] is None KEY[i] = key[j] print('KEY:', bytes(KEY).hex())
Four faults for the price of one.
One might think that the above attack only allows us to use the ciphertexts where a fault is introduced in the ninth round: those faulty ciphertexts with a Hamming distance of exactly four from the correct ciphertext.
However it turns out that the most useful fault is one introduced before MixColumns in the eight round:
A fault introduced in the eight round before MixColumns causes exactly one fault
in every column in the eight round: we get four faults for the effort of one.
This is illustrated below:
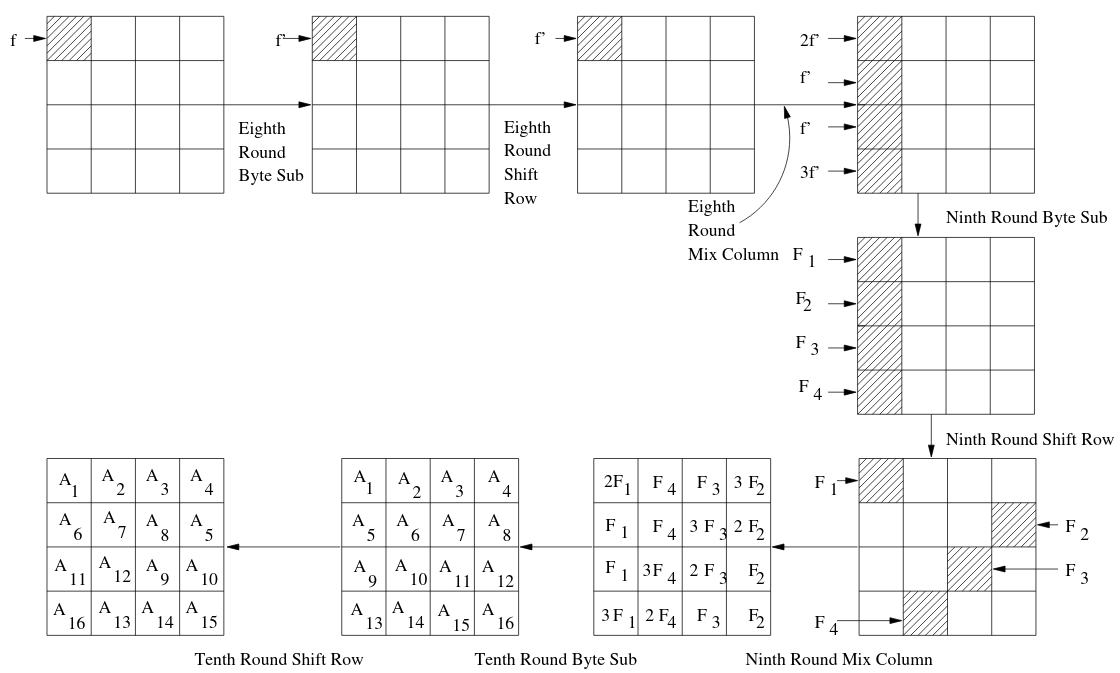
Hence such a faulty ciphertext will have a Hamming distance of exactly 16 from the correct ciphertext. Our program is also capable of taking advantage of these faults without any additional modifications. Now we are finally ready to recover the key:
Exercise.Use the program to recover the last round key.Solution (Click to Expand)
The last round key is:
13111d7fe3944a17f307a78b4d2b30c5
To recover the cipherkey itself we need to gain some insight into how the key schedule of AES-128 functions.
AES-128 key schedule
To recover the cipherkey (“the AES-128 key”), from the last round key we will need to understand the AES key-schedule. For those comfortable with C it might be easier to read the key-schedule code from the didactic AES implementation included in the repository (victim/aes.c).
The AES-128 key-schedule operates by splitting the 16 element/byte \( k^0_{0,0} k^0_{1,0} k^0_{2,0} k^0_{3,0} \) \( k^0_{0,1} k^0_{1,1} k^0_{2,1} k^0_{3,1} \) \( k^0_{0,2} k^0_{1,2} k^0_{2,2} k^0_{3,2} \) \( k^0_{0,3} k^0_{1,3} k^0_{2,3} k^0_{3,3} \) cipherkey into 4 “words” holding 4 field elements each. Then applies a function to the last word, adding the result (in \( \mathbb{F}_{2^8}^4 \)) to the first word, then cascading the change by adding every word to its successor (see the illustration below):
This process is repeated iteratively 10 times to produce the 11 required round keys: the first round key is the cipherkey and every intermediate result is a new round key.
Exercise.The AES key-schedule (image above) is invertible, regardless of whatRotWord,SubWordandRconare (they could be arbitrary functions): stare at the image above and convince yourself that the process can be inverted.Solution (Click to Expand)
The process is somewhat familiar to that of a generalized Feistel network. Recover:
- \( k^{0}_{0,3} \leftarrow k^{1}_{0,2} \oplus k^{1}_{0,3} \)
- \( k^{0}_{1,3} \leftarrow k^{1}_{1,2} \oplus k^{1}_{1,3} \)
- \( k^{0}_{2,3} \leftarrow k^{1}_{2,2} \oplus k^{1}_{2,3} \)
- \( k^{0}_{3,3} \leftarrow k^{1}_{3,2} \oplus k^{1}_{3,3} \)
- \( k^{0}_{0,2} \leftarrow k^{1}_{0,1} \oplus k^{1}_{0,2} \)
- \( k^{0}_{1,2} \leftarrow k^{1}_{1,1} \oplus k^{1}_{1,2} \)
- \( k^{0}_{2,2} \leftarrow k^{1}_{2,1} \oplus k^{1}_{2,2} \)
- \( k^{0}_{3,2} \leftarrow k^{1}_{3,1} \oplus k^{1}_{3,2} \)
- \( k^{0}_{0,1} \leftarrow k^{1}_{0,0} \oplus k^{1}_{0,1} \)
- \( k^{0}_{1,1} \leftarrow k^{1}_{1,0} \oplus k^{1}_{1,1} \)
- \( k^{0}_{2,1} \leftarrow k^{1}_{2,0} \oplus k^{1}_{2,1} \)
- \( k^{0}_{3,1} \leftarrow k^{1}_{3,0} \oplus k^{1}_{3,1} \)
Compute \( t_0, t_1, t_2, t_3 \leftarrow (\texttt{Rcon} \circ \texttt{SubWord} \circ \texttt{RotWord})(k^{0}_{0,3}, k^{0}_{1,3}, k^{0}_{2,3}, k^{0}_{3,3}) \)
- \( k^{0}_{0,0} \leftarrow t_0 \oplus k^{1}_{0,0} \)
- \( k^{0}_{1,0} \leftarrow t_1 \oplus k^{1}_{1,0} \)
- \( k^{0}_{2,0} \leftarrow t_2 \oplus k^{1}_{2,0} \)
- \( k^{0}_{3,0} \leftarrow t_3 \oplus k^{1}_{3,0} \)
Here is how RotWord, SubWord and Rcon actually works:
RotWord: Left-rotate the word. Given \( (w_1, w_2, w_3, w_4) \) return \( (w_2, w_3, w_4, w_1) \).
SubWord: Apply the S-box to every byte. Given \( (w_1, w_2, w_3, w_4) \) return \( (S[w_1], S[w_2], S[w_3], S[w_4]) \):
Rcon: Add (xor) a round constant into the first byte. Given \( (w_1, w_2, w_3, w_4) \) return \( (w_1 + \text{rcon}[r], w_2, w_3, w_4) \). Where \(r\) is the round number and \(\text{rcon}\) is the array [0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36].
Note: The Rcon constants are derived by repeatedly multiplying by the polynomial \( X \in \mathbb{F}_{2^8}\) (encoded as 0x02).
Exercise.Implement a script which takes the last round key of AES and recovers the cipherkey (equal to the first round key).Solution (Click to Expand)
See attacker/invert.py.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75#!/usr/bin/env python3 import sys import binascii rcon = [0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36] sbox = [ 0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76, 0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0, 0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15, 0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75, 0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84, 0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF, 0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8, 0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2, 0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73, 0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB, 0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79, 0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08, 0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A, 0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E, 0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF, 0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16 ] def words(key): assert len(key) == 16 return (key[0:4], key[4:8], key[8:12], key[12:]) def xor(a, b): assert len(a) == len(b) return bytes([x ^ y for (x, y) in zip(a, b)]) def rot(w): return w[1:] + bytes([w[0]]) def sub(w): return bytes([sbox[x] for x in w]) def invert(key, rcon): w1, w2, w3, w4 = words(key) w4 = xor(w4, w3) w3 = xor(w3, w2) w2 = xor(w2, w1) D = xor(bytes([rcon, 0, 0, 0]), sub(rot(w4))) w1 = xor(w1, D) return w1 + w2 + w3 + w4 if __name__ == '__main__': key = binascii.unhexlify(sys.argv[1]) for i, r in list(enumerate(rcon))[::-1]: key = invert(key, r) print('Round %d : %s' % (i, key.hex()))
Exercise.Use the program to obtain the cipherkey from the last round key.Solution (Click to Expand)
The cipherkey is:
000102030405060708090a0b0c0d0e0f
Independent Round Keys
In the attack above we made use of the fact that we can recover the cipherkey from the last round key. However even if AES used independent round keys we can recover all the remaining round keys by stripping rounds and keep applying differential fault attacks:
- Use the recovered round key to decrypt the last round of every ciphertext.
- Use the linear trick (see note) described in the AES encryption section to remove the last
MixColumns. - Mount a differential fault attack on the samples from this new (n - 1) round variant of AES
just as before and recover inverse
MixColumnsapplied to the new last round key. - Apply the
MixColumnsto the recovered key to obtain the actual round key.
Repeat for every round.
Exercise.Convince yourself that this works.