HalfFeed
The HalfFeed service allows us to encrypt almost any message. The only restriction is that it cannot contain the string “cat flag”:
def encrypt(halffeed):
global nonce
P = recv_data('plaintext')
if b'cat flag' in P:
print('[EXCEPTION] Invalid Command "cat flag"')
exit()
C, T = halffeed.encrypt(nonce.to_bytes(16, byteorder='big'), P)
send_data('ciphertext', C)
send_data('tag', T)
nonce += 1
We can also provide a ciphertext, that is split on “;”. If any of the segments is “cat flag” we win:
def execute(halffeed):
N = recv_data('nonce')
C = recv_data('ciphertext')
T = recv_data('tag')
P = halffeed.decrypt(N, C, T)
if P is not None:
cmds = P.split(b';')
for cmd in cmds:
if cmd.strip() == b'cat flag':
with open('./flag') as f:
print(f.read())
else:
print('[EXCEPTION] Unknown Command')
else:
print('[EXCEPTION] Authentication Failed')
exit()
We have our job cut out for us.
Encryption is done using some Frankenstein mode with a AES-CTR-like encryption with a AES-CBC-MAC-like authentication. The relevant parts of the code is provided below, though it is easier to read the description that follows:
from Crypto.Cipher import AES
def aes_encrypt(key, data):
assert isinstance(key, bytes) and isinstance(data, bytes)
assert len(key) == 16 and len(data) == 16
aes = AES.new(key, AES.MODE_ECB)
return aes.encrypt(data), aes.encrypt(key)
def pad(data):
assert isinstance(data, bytes)
assert len(data) <= 16
if len(data) != 16:
data += b'\x01' + b'\x00' * (15 - len(data))
return data
class HalfFeed(object):
...
def feed_plus(self, tag, data):
assert isinstance(tag, bytes) and isinstance(data, bytes)
assert len(tag) == 16 and len(data) <= 16
enc_data = bytes(b1 ^ b2 for b1, b2 in zip(tag, data))
feed_data = pad(data)[:8] + pad(enc_data)[8:]
tag = bytes(b1 ^ b2 for b1, b2 in zip(tag, feed_data))
return tag, enc_data
...
def encrypt(self, nonce, plaintext):
assert isinstance(nonce, bytes) and isinstance(plaintext, bytes)
assert len(nonce) == 16
delta = len(plaintext) % 16
delta = delta.to_bytes(16, byteorder='little')
Kn, _ = aes_encrypt(self.key, nonce)
T, K = aes_encrypt(Kn, nonce)
ciphertext = b''
for i in range(0, len(plaintext), 16):
T, block = self.feed_plus(T, plaintext[i:i+16])
ciphertext += block
T, K = aes_encrypt(K, T)
T = bytes(b1 ^ b2 for b1, b2 in zip(T, delta))
T, _ = aes_encrypt(K, T)
return ciphertext, T
The feed_plus operation does:
\[ \text{enc_data} \leftarrow \text{tag} \ \oplus \ \text{data} \] \[ \text{tag} \leftarrow \text{tag} \ \oplus \ (\text{data[:8]} \ |\!| \ \text{enc_data[8:]}) \]
This can be simplified into:
\[ \text{enc_data} \leftarrow \text{tag} \ \oplus \ \text{data} \] \[ \text{tag} \leftarrow \text{enc_data[:8]} \ |\!| \ \text{data[8:]} \]
The tag is then encrypted, before processing the next block: \[ \text{tag} \leftarrow \text{AES}_{k_i}(\text{tag}) \] \[ k_{i+1} \leftarrow \text{AES}_{k_i}(k_i) \] Visually the tag generation operates as follows:
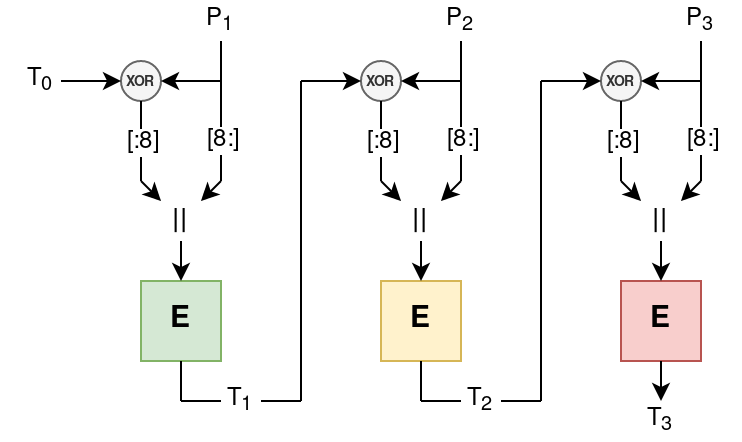
The IV affects not only \( T_0 \), but also \( k_0 \) and hence the “key-schedule” for the encryption (indicated above with different colored boxes). However when we reconnect the IV is reset, hence we can trick the server into reusing the same IV. When we encrypt two different plaintexts with the same IV, the key-schedule and initial tag will be the same. Illustrated below:
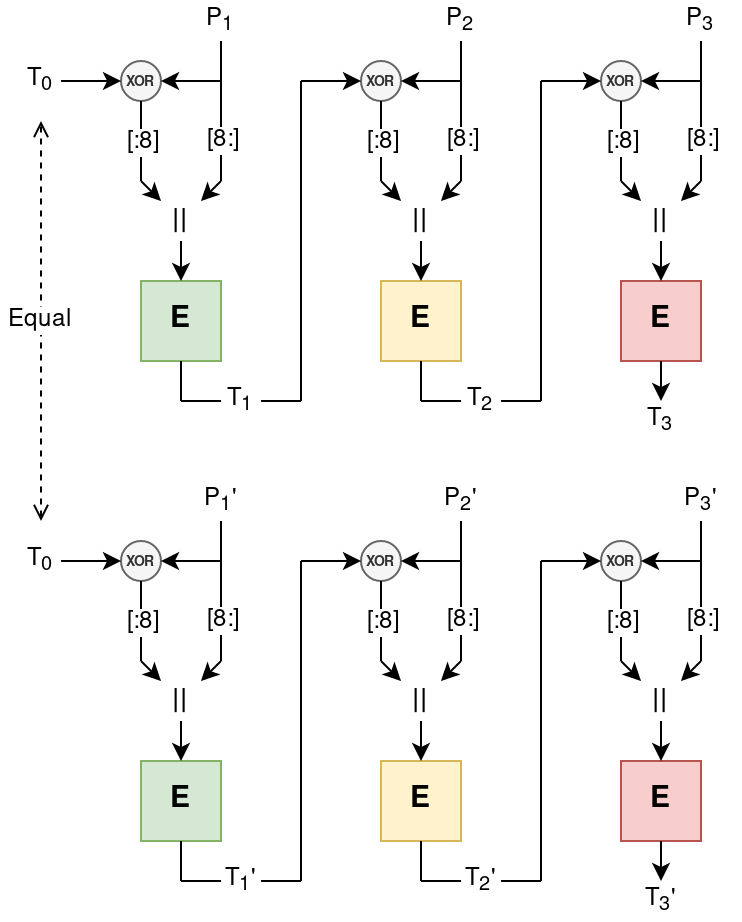
We can then “glue” the two ciphertexts with the same IV together, by having a prefix from the first message, a specially crafted block, then the postfix from the second message. The resulting tag will be that of the second message, \( T_3’ \):
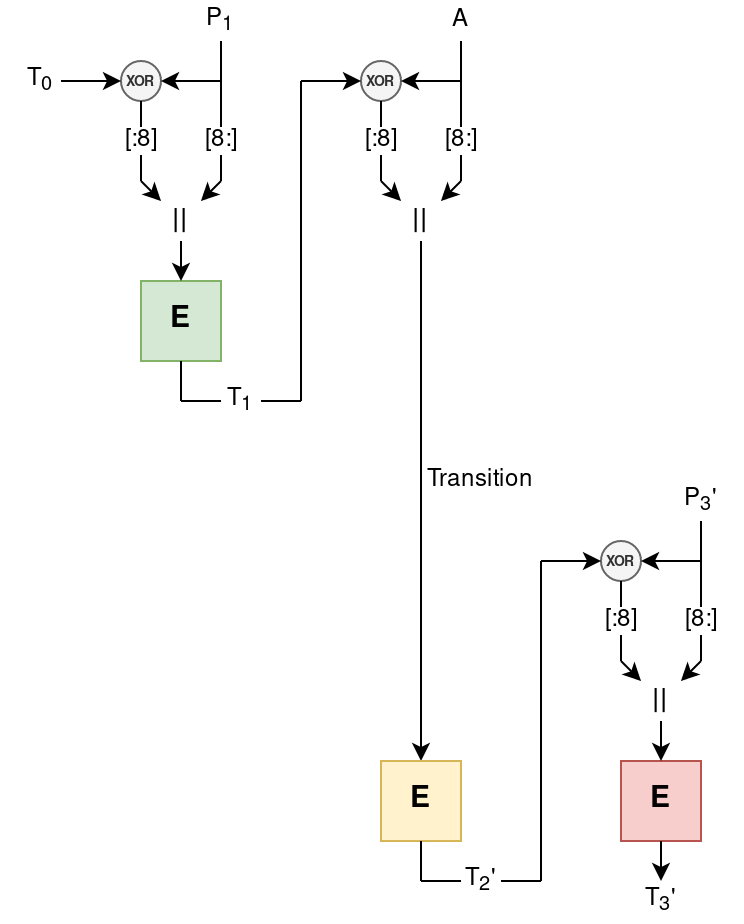
By picking \( A = \Delta \oplus P_2 \), where \( \Delta = (C_2 \oplus C_2’)\text{[:8]} + (P_2 \oplus P_2’)\text{[8:]} \). Note that we can manipulate the plaintext \( A \) by xoring the same difference into the ciphertext \( C_2 \), since it is completely linear:
def glue(pair1, pair2, i):
P1, C1, T1 = pair1
P2, C2, T2 = pair2
assert len(C1) == len(P1)
assert len(C2) == len(P2)
assert len(C1) == len(C2)
P1 = blocks(P1)
P2 = blocks(P2)
C1 = blocks(C1)
C2 = blocks(C2)
delta = xor(
C1[i],
C2[i]
)[:8] + xor(P1[i], P2[i])[8:]
P = list(P2)
C = list(C2)
P[i] = xor(P1[i], delta)
C[i] = xor(C1[i], delta)
for j in range(i):
P[j] = P1[j]
C[j] = C1[j]
return join(P), join(C), T2
We make use of this by requesting a number of encryptions of 3 block messages under the same IV, where \( P_1 = r \ |\!| \ \text{";cat fla"} \) for random \( r \):
def block():
v = os.urandom(8) + b';cat fla'
assert len(v) == 16
return v
def plaintext():
pt = b'cat flag'
while b'cat flag' in pt:
pt = block() + os.urandom(32)
return pt
Then we glue every pair of ciphertexts together and hope that \( A \) starts with “g;”. In which case the plaintext will contain “;cat flag;” as desired:
def mutate(pairs, pair2):
print('pairs:', 2 * len(pairs))
for i in range(len(pairs)):
pair1 = pairs[i]
P, C, T = glue(pair1, pair2, 1)
if b'cat flag;' in P:
return (P, C, T)
P, C, T = glue(pair2, pair1, 1)
if b'cat flag;' in P:
return (P, C, T)
return None
By the birthday paradox we need \( \approx \sqrt{ 2^{16} } = 256 \) plaintext/ciphertexts pairs
for the attack to succeed.
After “glueing” together such a ciphertext and tag, we simply (manually, not in doit.py) send this to the server and obtain the flag:
CODEGATE2020{F33D1NG_0N1Y_H4LF_BL0CK_W1TH_BL0CK_C1PH3R}
The challenge files and exploit can be found on github.